類神經網路—反向傳播法(四): 揭開反向傳播法神秘面紗

前言

先前在梯度下降法的文章中有提到在步驟二的部分，是要求取當前權重的梯度，我們是直接給定了梯度往下做計算，也因此實際上會面臨到梯度如何給定的問題，那我們該如何求得當前權重所對應的梯度呢?這件事情正是反向傳播法的核心精神，就是利用系統化的數學方法，有根據的去求取每一個當前權重的梯度值。

範例

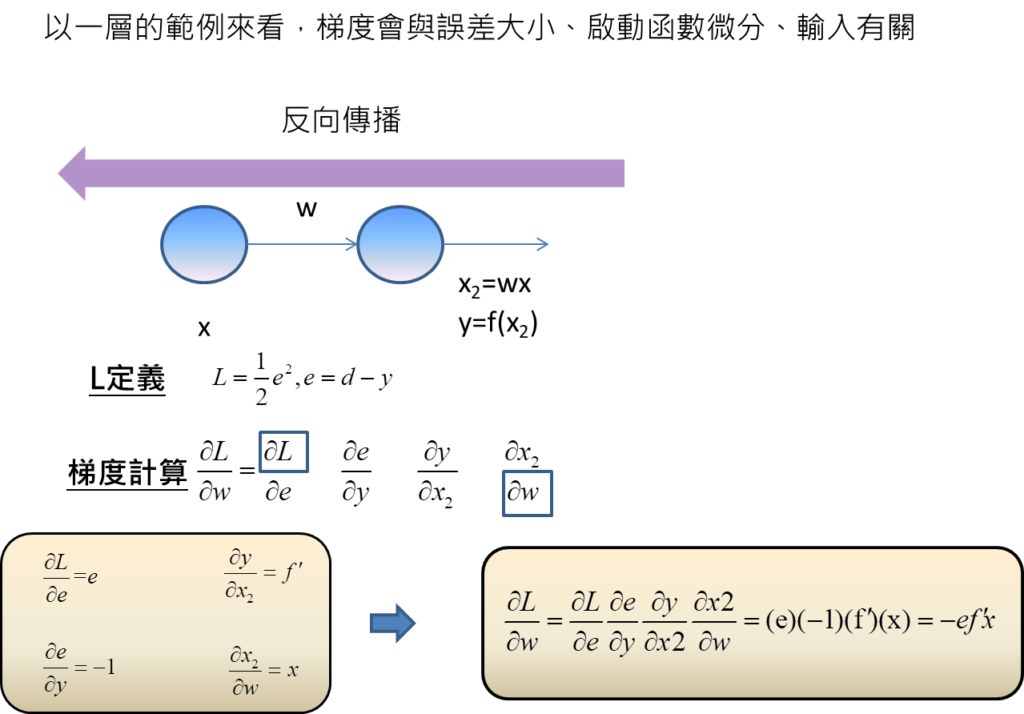
假設現在只有兩層的類神經網路，分別對應到一個節點，左邊層為輸入，右邊層為輸出，這時候可以了解到當輸入為x，經過權重w的計算，在節點輸出部分即為x2=wx，不過還要取啟動函數才會是最終輸出，因此，最終輸出y為f(x2)。

這邊的話我們要定義L代表的是損失，會等於0.5倍的誤差e平方，而誤差代表標準解答d與預測輸出y的差距。

為什麼我們需要有L來定義損失呢?這是因為e可正可負，難以衡量損失大小，因此才會透過L的計算，才能更清楚了解到每個權重所計算出來的損失。

接下來，我們待求得的梯度定義即為L對w的微分。

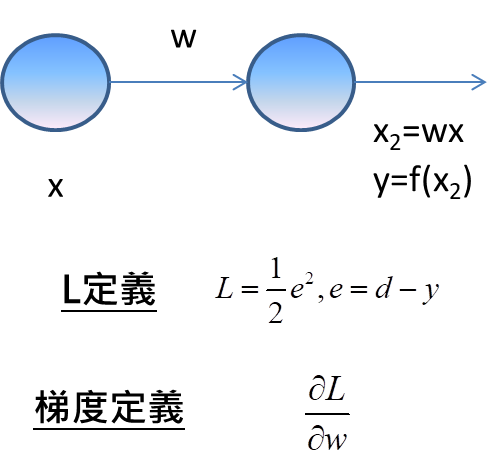
我們該如何求得梯度呢?就要從數學的關係式去求得，因為L與w的關係，是函數的函數的…關係，L並不是w直接的函數關係，所以在求得微分上，需要採用鎖鏈法則，將微分展開多項相乘才能得到結果。

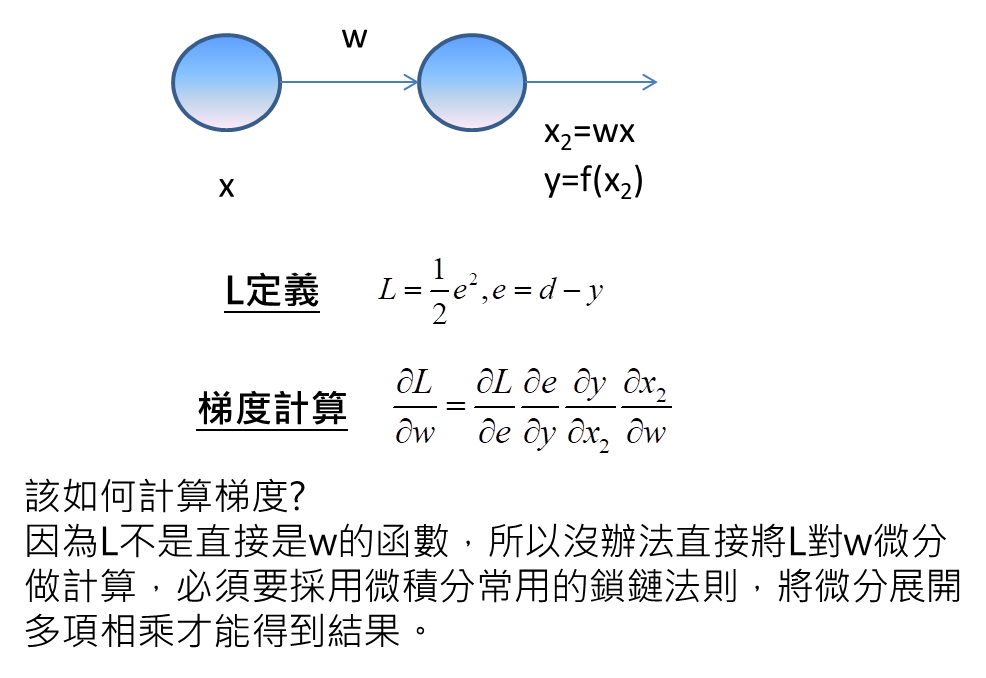
鎖鏈法則的意思是要將這個微分，拆成有若干直接函數關係的情況，才能微分，意思也就是說這邊拆成四項，第一項L與e為直接函數關係，因為L正等於1/2*e平方。第二項e與y有直接函數關係，因為e=d-y。第三項y與x2有直接函數關係，因為y=f(x2)。第四項x2與w有直接函數關係，因為x2=wx。

透過鎖鏈法則，將有直接函數關係的才能微分，再將這些微分相乘，我們就可計算出梯度。

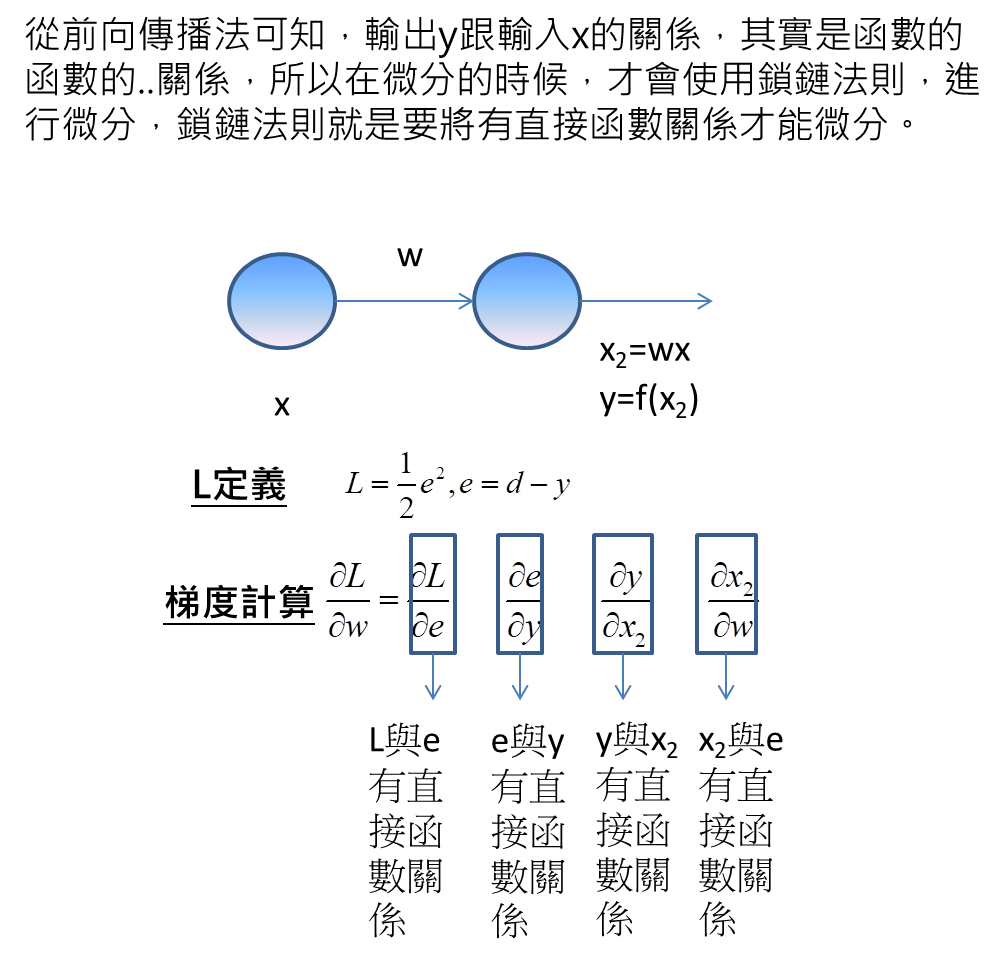
從上面鎖鏈法則的計算可發現到，第一項微分的分子一定是L，最後一項微分的分母一定是w。

L的計算，因為要將真實解答d與預測輸出y相比，因此，對於L的計算是在類神經網路的最右邊，而w的計算是位在類神經網路左邊的位置，這代表為了要計算梯度，需要從右到左不斷計算每一項的微分，才能得到梯度的資訊，也因為這樣的特性，要從最後往前計算的特性，這個方法就稱作反向傳播法。

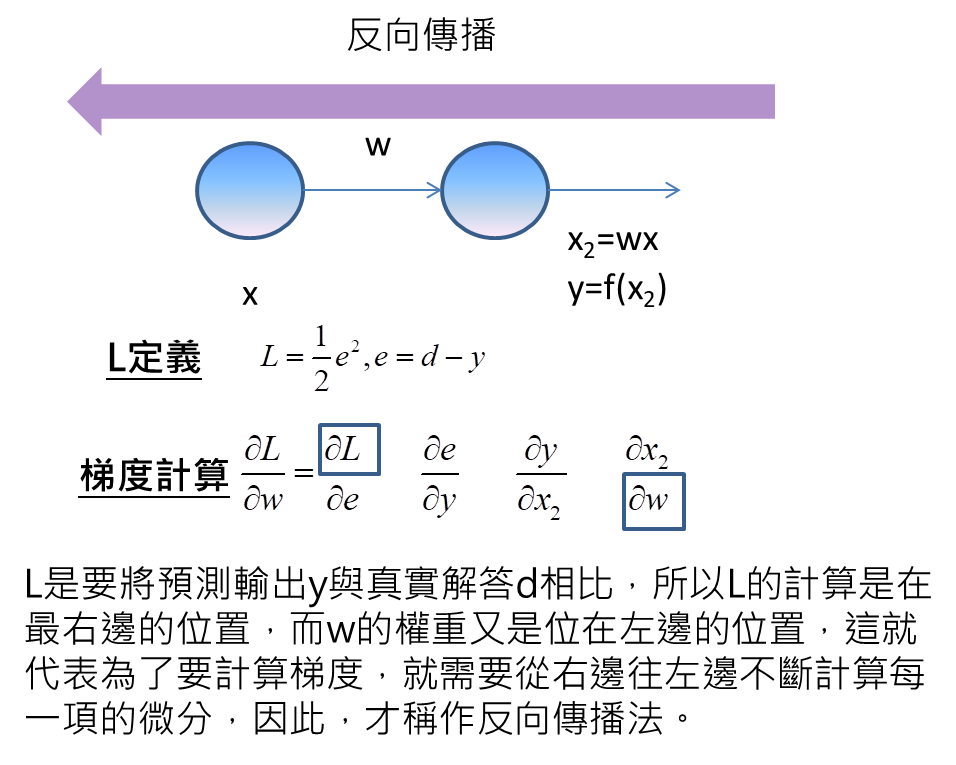
最後，我們進一步去求得每一項的微分，L對e的微分即為e，e對y的微分即為-1，y對x2的微分等於啟動函數f的微分，x2對w的微分為x。

將這些結果代到鎖鏈法則當中，即可知道梯度會與誤差大小，啟動函數的微分以及輸入有關。

總結

梯度的計算，在數學上因為輸出與輸入為若干的函數的函數的…關係，所以計算梯度時就會採用鎖鏈法則計算。而採用鎖鏈法則計算之後，我們就可了解到必須要從類神經網路的末端往前端不斷的計算每一項的微分才能得到梯度，因為計算方向是從後到前，因此方法又稱作反向傳播法。

而最後以一層的範例來計算，可以了解到梯度即為當前誤差，啟動函數微分，輸入有關，這三者大小的變化，就會影響梯度的大小。簡單來說就是透過誤差，啟動函數的微分，輸入，我們就可以知道梯度的方向，我們根據負梯度的方向下山，就可以最快速達到損失函數的谷底。才能有效得到訓練完成的AI模型。

[參考資料]:

1.快速反應機制─類神經網路

2.機器學習與人工神經網路(二)：深度學習(Deep Learning)

3.機器學習的衰頹興盛：從類神經網路到淺層學習

[相關文章]:

1.類神經網路(Deep neural network, DNN)介紹

2.類神經網路—揭開網路架構調整秘辛

3.類神經網路—啟動函數介紹

4.類神經網路—前向傳播法

5.類神經網路—反向傳播法(一): 白話文帶您了解反向傳播法

6.類神經網路—反向傳播法(二): 淺談梯度

7.類神經網路—反向傳播法(三): 五步驟帶您了解梯度下降法

8.類神經網路—反向傳播法(四): 揭開反向傳播法神秘面紗

9.機器學習訓練原理大揭秘：六步驟帶您快速了解監督式學習的訓練方法

10.類神經網路—反向傳播法(五): 用等高線圖讓您對學習率更有感

[延伸閱讀]:

1.卷積類神經網路(Convolution neural network,CNN)介紹

2.遞迴類神經網路(Recurrent neural network,RNN)介紹

3.淺談最近非常火紅的ChatGPT背後可能原理機制為何?