類神經網路—啟動函數介紹(二): 回歸 vs. 分類: 線性函數與Tanh函數之原理探索

延續先前啟動函數的介紹，此處要再跟大家介紹兩個啟動函數，也就是linear和tanh函數。

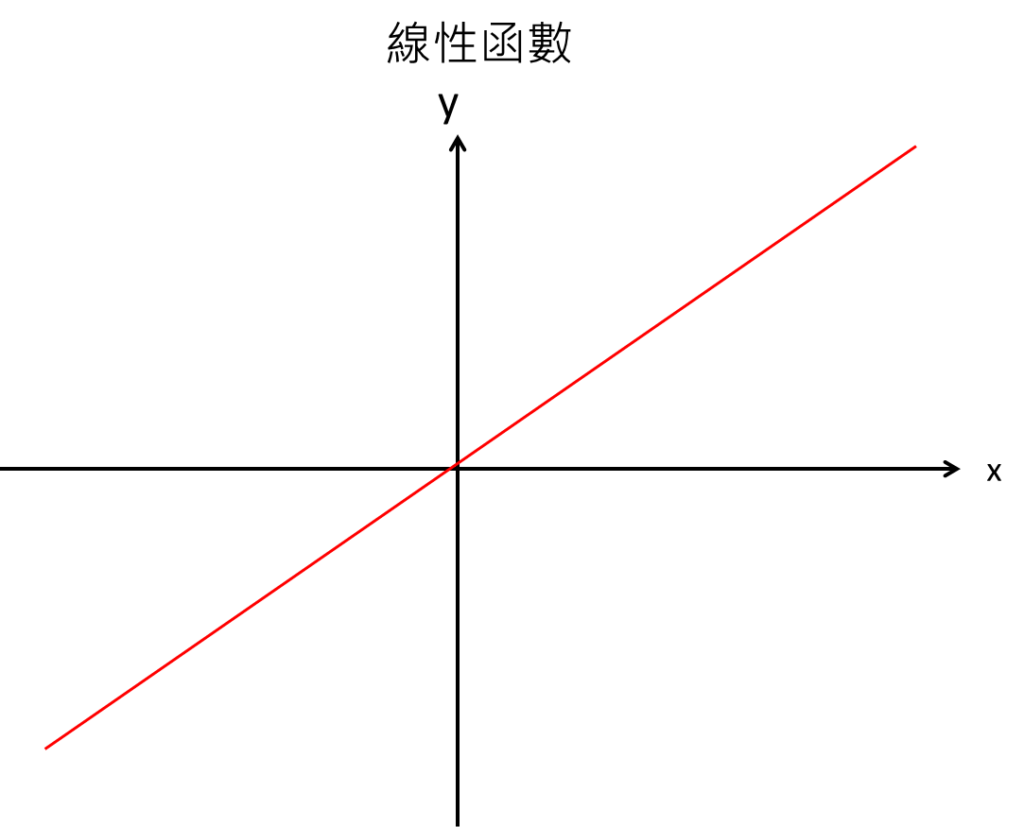
線性函數的特性是x與y增長速度相同，這代表其實經由線性函數的運算後，x就會等於y。當一個節點輸出的時候，取完線性啟動函數，就仍然會等於原本的輸出。此函數通常會應用在輸出層，會應用在處理回歸的問題上。這是由於回歸問題，最終輸出端是要給出一個數值，為了要較穩定得到結果，就會取線性函數，代表原本計算出來的值是多少就是多少。

舉個例子，假設輸出層的啟動函數是採用Relu函數，那麼有可能在某些情境下。預測的時候，只要輸出節點的數值為負，再經由Relu函數的運算，就會直接為零，進而無法看出回歸出來的數值是多少。

因為在輸出層的部分，以回歸問題來看，僅僅只是要得到訊號的加總，沒有必要再去篩選某個節點重不重要。因為輸出層通常是只有一個節點，再篩選掉就為零了。所以為了穩定性，就會選擇線性函數。

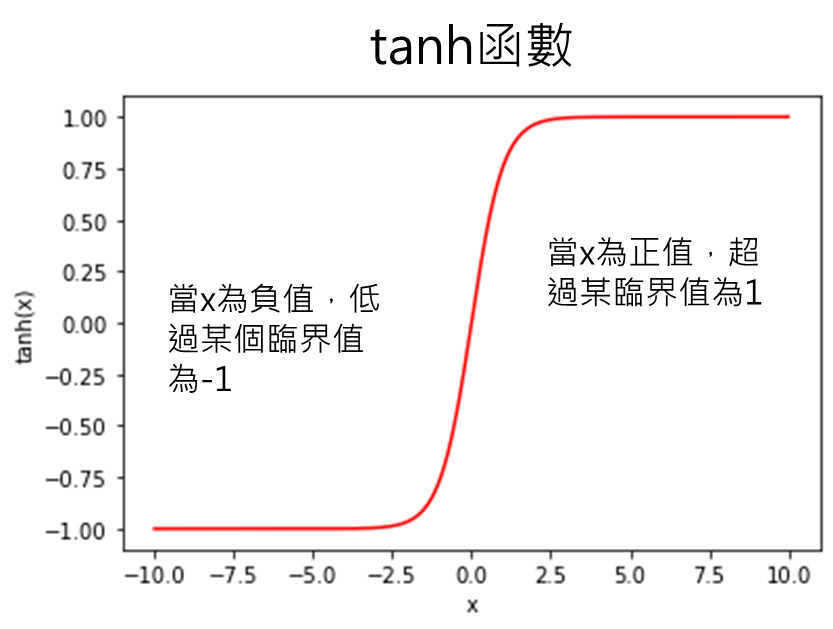
tanh函數，特性在於當x為正值，超過某臨界值就會為1，當x為負值，低過某個臨界值就為-1，以1跟-1為界線，用在二元分類的問題。跟先前介紹的sigmoid相比，sigmoid則是用0~1之間來作二元分類。這兩者啟動函數都是用在輸出層，用以決定最終分類類別為何。這兩者函數的特性相似，只是差別在於sigmoid函數是以0.5當正負樣本的分界點，而tanh函數是以0當作分界點。

[參考資料]:

1.快速反應機制─類神經網路

2.機器學習與人工神經網路(二)：深度學習(Deep Learning)

3.機器學習的衰頹興盛：從類神經網路到淺層學習

[相關文章]:

1.類神經網路(Deep neural network, DNN)介紹

2.類神經網路—揭開網路架構調整秘辛

3.類神經網路—啟動函數介紹

4.類神經網路—前向傳播法

5.類神經網路—反向傳播法(一): 白話文帶您了解反向傳播法

6.類神經網路—反向傳播法(二): 淺談梯度

7.類神經網路—反向傳播法(三): 五步驟帶您了解梯度下降法

8.類神經網路—反向傳播法(四): 揭開反向傳播法神秘面紗

9.機器學習訓練原理大揭秘：六步驟帶您快速了解監督式學習的訓練方法

10.類神經網路—反向傳播法(五): 用等高線圖讓您對學習率更有感

[延伸閱讀]:

1.卷積類神經網路(Convolution neural network,CNN)介紹

2.遞迴類神經網路(Recurrent neural network,RNN)介紹

3.淺談最近非常火紅的ChatGPT背後可能原理機制為何?