特徵歸一化(feature normalization)
前言
機器學習並不像深度學習可以自動辨別關鍵特徵。機器學習在訓練之前,需要針對輸入進行特徵工程才會讓模型有好的訓練效果。特徵工程有許多種作法,本篇文章帶您了解常用的特徵工程—特徵歸一化的方法。
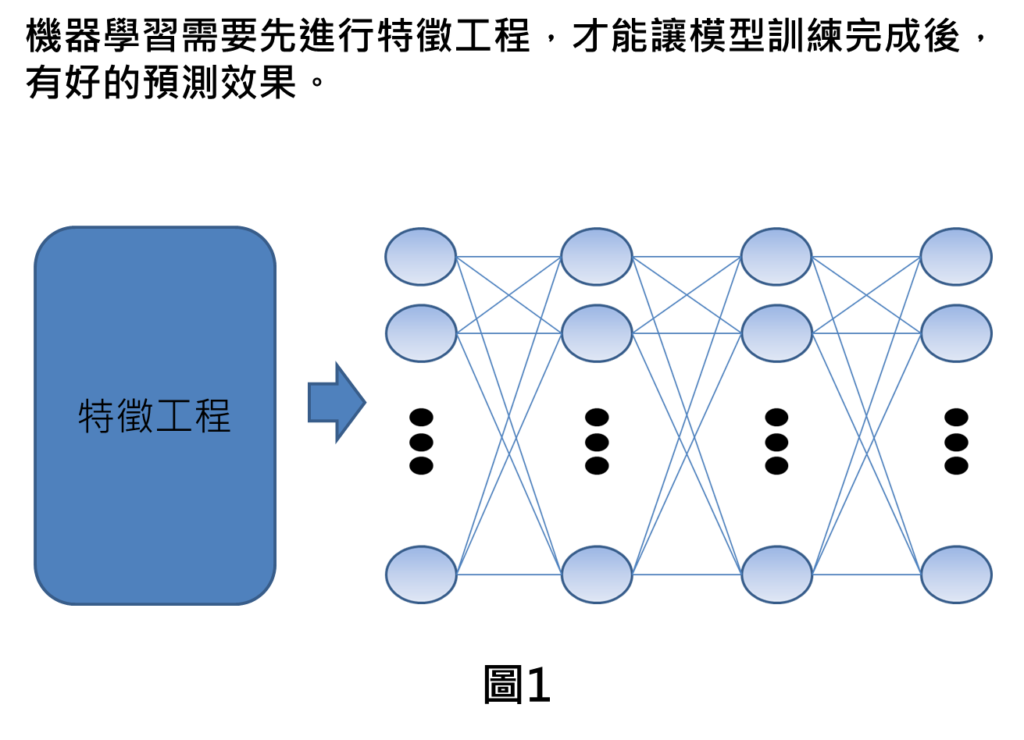
特徵歸一化(feature normalization)介紹
為何需要特徵歸一化呢? 之所以會有這樣的需求,是機器在訓練的過程中,同時存在許多特徵,而特徵與特徵之間數值範圍差異大,將影響機器學習的訓練效果,因此,我們需要特徵歸一化來改善這樣的問題。
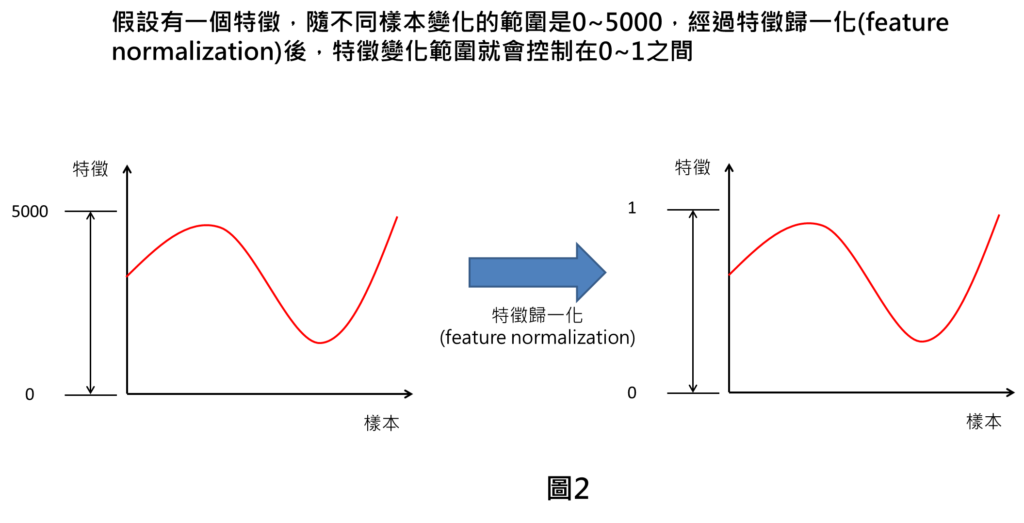
到底特徵歸一化是什麼呢?舉例來說,假設有一個特徵隨不同樣本變化的數值範圍落在0~5000,而特徵歸一化在做的事情就是讓這個特徵的數值範圍全部控制在0~1之間。
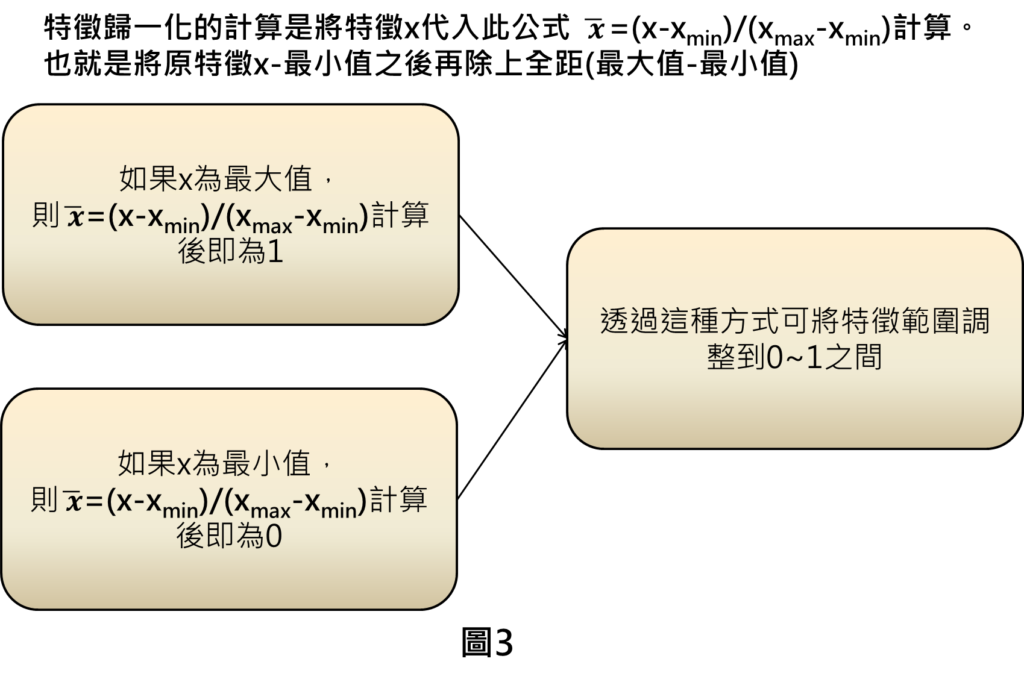
特徵歸一化的作法是將原特徵x扣掉最小值再除上全距來得到,透過這樣的作法就可以讓特徵範圍調整到0~1之間,舉例來說,假設特徵x為最大值,透過特徵歸一化的計算後,則會得到1;假設特徵x為最小值,則特徵歸一化計算後,會得到0,其他特徵數值必定介於最大與最小值之間,因此,可將特徵範圍調整到0~1之間。
特徵歸一化(feature normalization)效果
到底有特徵歸一化跟沒有特徵歸一化的訓練效果差在哪裡呢?
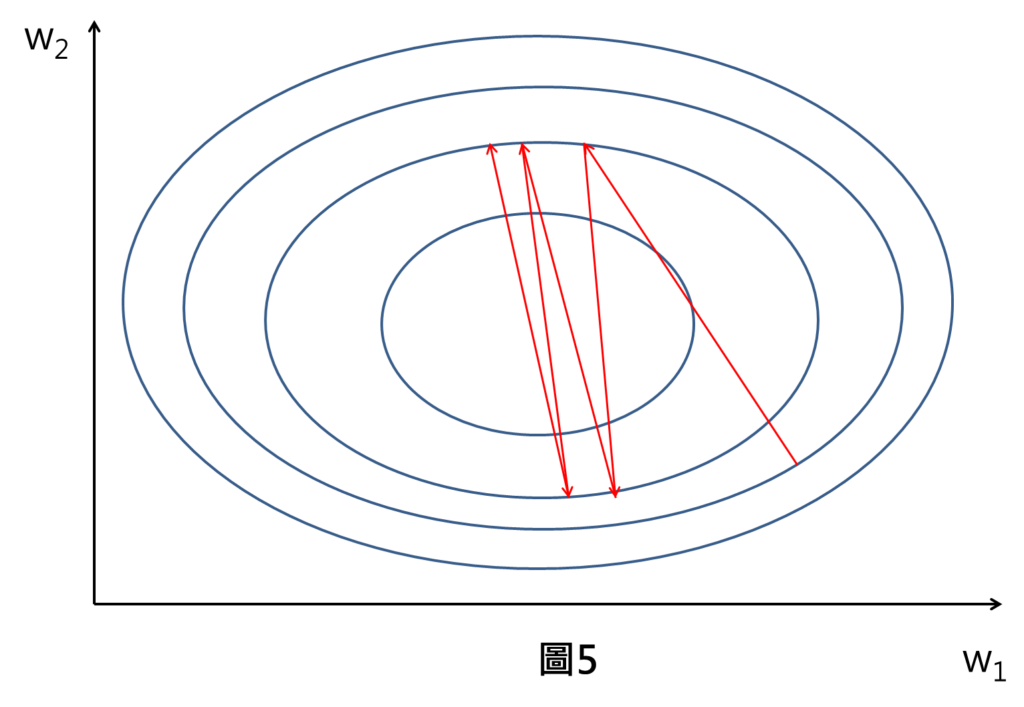
假設一個情形,我們輸入的特徵只有兩個x1與x2,這兩個特徵的數值範圍差異很大,像是x1範圍落在0~1,x2範圍落在0~1000,這時候進行梯度下降的權重差異也很大,像是w1為0~1,w2為0~0.001,此時,整個損失空間為橢圓形。(這邊的損失空間圖形以等高線方式呈現,也就是同一個橢圓形上,代表有相同的損失數值,在正中間為谷底代表是損失最低點。)

當我們以較大的學習率進行梯度下降,權重移動的方向會沿著負梯度方向(垂直等高線的方向)進行移動,然後我們發現到機器在訓練過程中,損失是沒有辦法有效下降到最低點,只有不斷震盪的現象。
這樣會使得機器在訓練時,收斂速度非常慢,而且訓練完成後,權重也未必會落在損失最低點,使得訓練完成的模型預測效果不好。
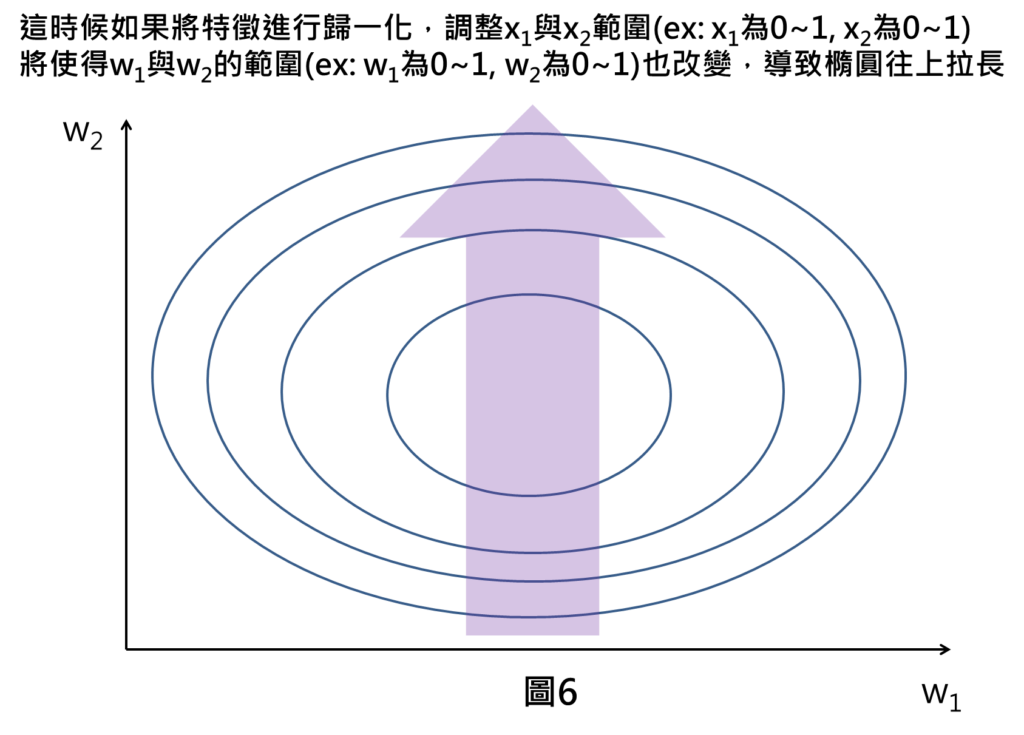
這時候如果我們將特徵進行歸一化,將兩特徵數值範圍調整到0~1之間,將使得w1與w2的數值範圍也隨之改變,舉例來說,原本x2的數值範圍為0~1000,w2範圍為0~0.001之間,而現在x2的數值範圍調整為0~1之間,w2範圍也恢復正常落在0~1之間,造成整個w2範圍變大,導致整個損失空間橢圓形往上拉長。
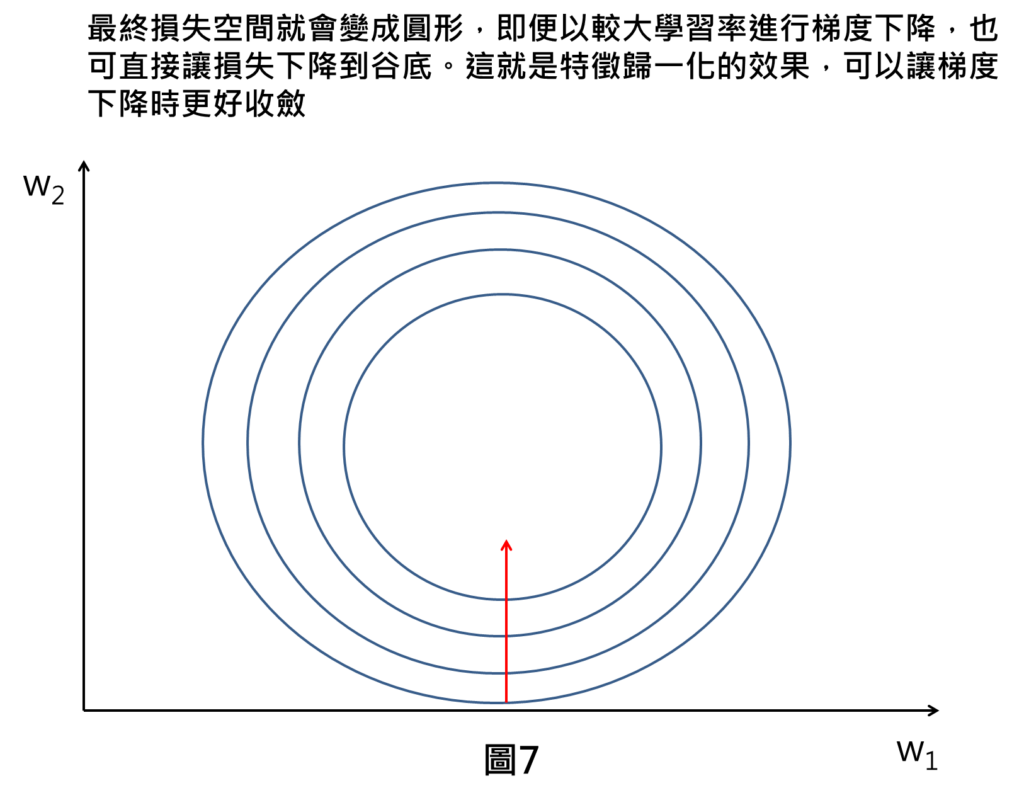
最終損失空間就會變成圓形,圓形的好處是在任意點進行梯度下降,其梯度方向皆指向圓心(即為谷底),即便在較大的學習率下降,損失也可以快速下降至谷底,使得機器訓練時有更好的收斂效果。
結論
本篇文章帶您了解特徵歸一化的重要性,其中包含:
1.特徵歸一化的作法: 透過最大值與最小值調整比例的計算公式,可讓特徵範圍落在0~1之間。
2.特徵歸一化的效果: 可讓機器在訓練時,有更好的收斂效果。
想要看更多AI文章,更了解學習脈絡,請參考AI學習路線圖。
[參考資料]:
2.機器學習與人工神經網路(二):深度學習(Deep Learning)
[類神經網路基礎系列專文]:
1.類神經網路(Deep neural network, DNN)介紹
3.類神經網路—啟動函數介紹(一): 深入解析Relu與Sigmoid函數:如何影響類神經網路的學習效果?
4.類神經網路—啟動函數介紹(二): 回歸 vs. 分類: 線性函數與Tanh函數之原理探索
5.類神經網路—啟動函數介紹(三): 掌握多元分類的核心技術:不可不知的softmax函數原理
6.類神經網路—啟動函數介紹(四): 如何選擇最適當的啟動函數?用一統整表格讓您輕鬆掌握
8.類神經網路—反向傳播法(一): 白話文帶您了解反向傳播法
10.類神經網路—反向傳播法(三): 五步驟帶您了解梯度下降法
11.類神經網路—反向傳播法(四): 揭開反向傳播法神秘面紗
12.機器學習訓練原理大揭秘:六步驟帶您快速了解監督式學習的訓練方法
13.類神經網路—反向傳播法(五): 用等高線圖讓您對學習率更有感
[機器學習基礎系列專文]:
1.機器學習訓練原理大揭秘:六步驟帶您快速了解監督式學習的訓練方法
[類神經網路延伸介紹]:
1.卷積類神經網路(Convolution neural network,CNN)介紹
2.遞迴類神經網路(Recurrent neural network,RNN)介紹
[ChatGPT系列專文]: